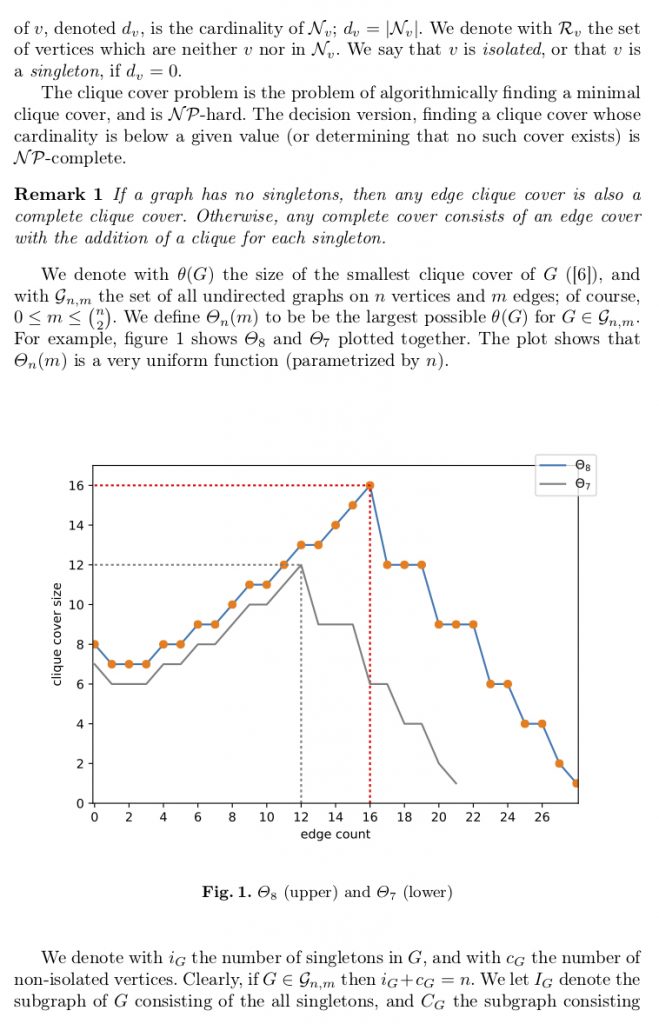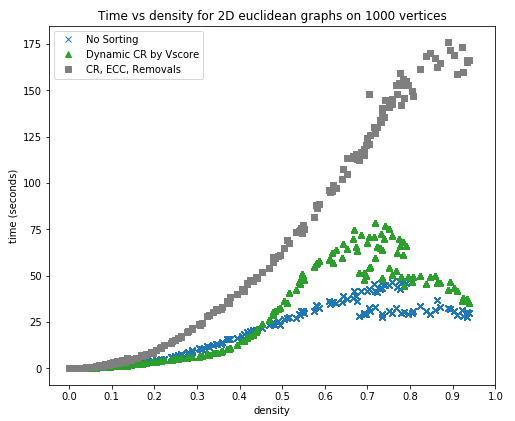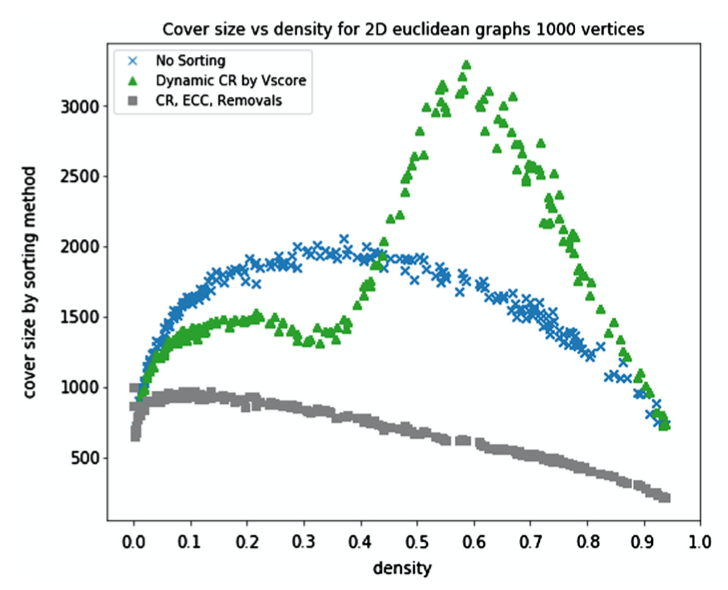
In May 2018, Ryan McIntyre defended his masters thesis (at CSUCI under my supervision) on Bounding the size of minimal clique covers. We followed up with a publication of the results in the Journal of Discrete Algorithms (https://doi.org/10.1016/j.jda.2018.03.002) [post], and now, two years later, our results are cited and built upon in an interesting paper Static beam placement and frequency plan algorithms for LEO constellations (https://doi.org/10.1002/sat.1345) written by an Astronautics research group at MIT.
What is interesting about this is the serendipitous manner in which results build on each other: our result consisted in a partial solution to an original problem in combinatorics posed by the itinerant mathematician Paul Ërdos (posed in the mid 1960s), which we then used to partially solve a problem related to string indeterminates (also in this case working on previous results of Joel Helling [post]), which are related to genetics. Now, our work is being used to solve the problem of satellite allocation.