Tag: Joel Helling

Our results in “Edge Covers” picked up by an Astronautics research group at MIT

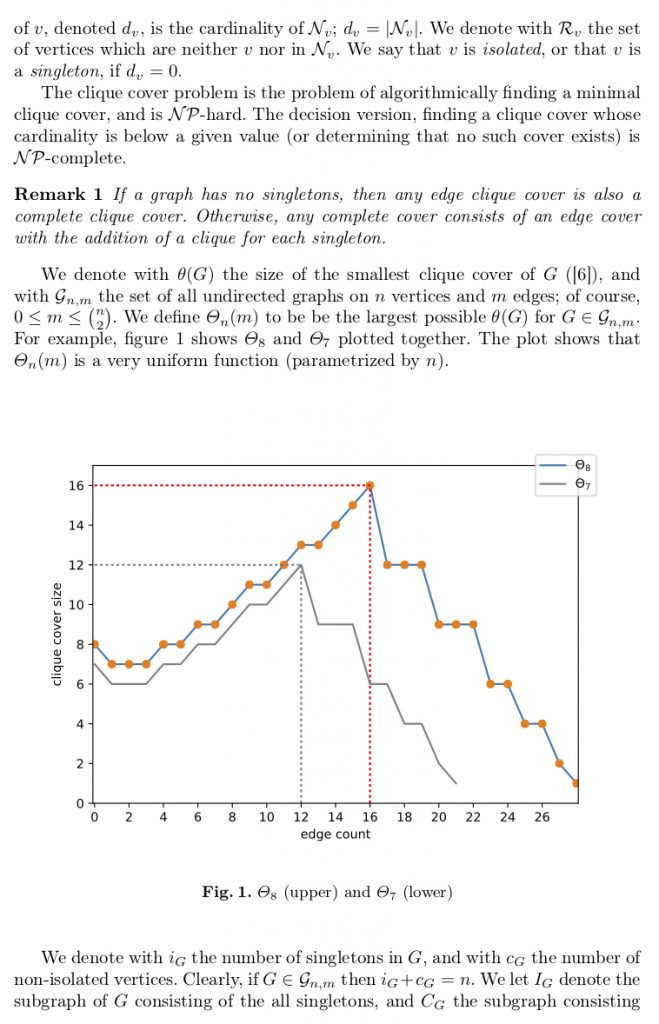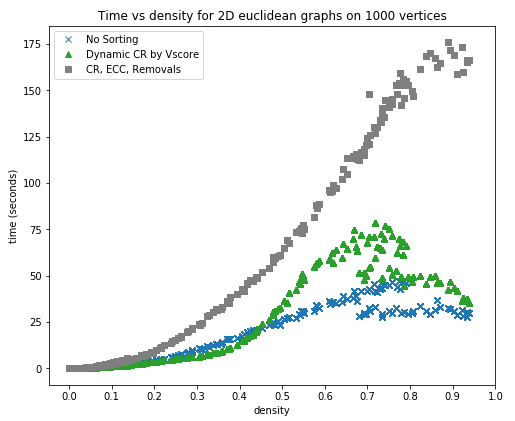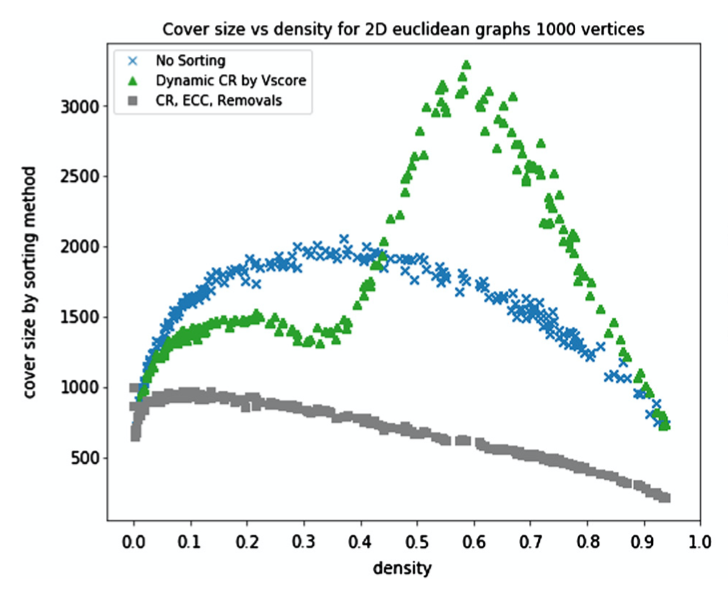
In May 2018, Ryan McIntyre defended his masters thesis (at CSUCI under my supervision) on  Bounding the size of minimal clique covers. We followed up with a publication of the results in the Journal of Discrete Algorithms (https://doi.org/10.1016/j.jda.2018.03.002) [post], and now, two years later, our results are cited and built upon in an interesting paper Static beam placement and frequency plan algorithms for LEO constellations (https://doi.org/10.1002/sat.1345) written by an Astronautics research group at MIT.

What is interesting about this is the serendipitous manner in which results build on each other: our result consisted in a partial solution to an original problem in combinatorics posed by the itinerant mathematician Paul Ërdos (posed in the mid 1960s), which we then used to partially solve a problem related to string indeterminates (also in this case working on previous results of Joel Helling [post]), which are related to genetics. Now, our work is being used to solve the problem of satellite allocation.

Paper with Ryan McIntyre to appear in the Journal of Discrete Algorithms

Happy to announce that Ryan McIntyre’s masters thesis results, An improved upper bound and algorithm for clique covers (prelim), will be published as our joint paper in Journal of Discrete Algorithms.

Our paper is on indeterminate strings, which are important for their applicability in bioinformatics. (They have been considered, for example, in Christodoulakis 2015  and Helling 2017.)

An interesting feature of indeterminate strings is the natural correspondence with undirected graphs. One aspect of this correspondence is the fact that the minimal alphabet size of indeterminates representing any given undirected graph corresponds to the size of the minimal clique cover of this graph. This paper first considers a related problem proposed in Helling 2017: characterize $latex\Theta_n(m)$, which is the size of the largest possible minimal clique cover (i.e., an exact upper bound), and hence alphabet size of the corresponding indeterminate, of any graph on $latex n$ vertices and $latex m$ edges. We provide improvements to the known upper bound for $latex \Theta_n(m)$. Helling 2017 also presents an algorithm which finds clique covers in polynomial time. We build on this result with an original heuristic for vertex sorting which significantly improves their algorithm’s results, particularly in dense graphs.

This work was the result of building on Helling 2017 (see this post) and of a year of research undertaken by Ryan McIntyre under my (Michael Soltys) supervision at the California State University Channel Islands.

An article from the CSUCI news center about this work can be found here.

Indeterminates in London

Today my masters student Joel Helling presented our joint work, Constructing an Indeterminate String from its Associated Graph,  co-authored with P.J. Ryan, W.F. Smyth, at the LSD & LAW 2017 conference. This work started with the visit of W.F. Smyth at CSU Channel Islands in March 2016 – see here, when Joel, Bill and I started working on an initial algorithm designed by Joel; this algorithm computed a labeling for a graph such that any two nodes that shared an edge would also share a label, and would not share a label otherwise. Of course, the easy way to do this is to assign each edge a unique label; but there are better ways of doing it, in the sense that fewer labels may be required (for example, imagine a clique: then a single label would do it). This problem is directly related to indeterminate strings; strings that arise in bio-informatics, where certain positions may consist of several possible symbols. For example, {a,b}ab{a,b,c}{b,c}a, where the first position is not determined (it could be a or b), the second position is a, the third b, the fourth is again not determined (it could be a or b or c), etc. Such strings are well suited to represent genetic
information which often contains “noise”. The paper is now accepted for publication in Elsevier’s journal of Theoretical Computer Science,  as well as presented by Joel at the conference.

I would like to express my gratitude to the British Royal Society for awarding us an exchange grant, CSU Channel Islands / King’s College London, which financed the trip of Joel Helling.

CI Facebook post.