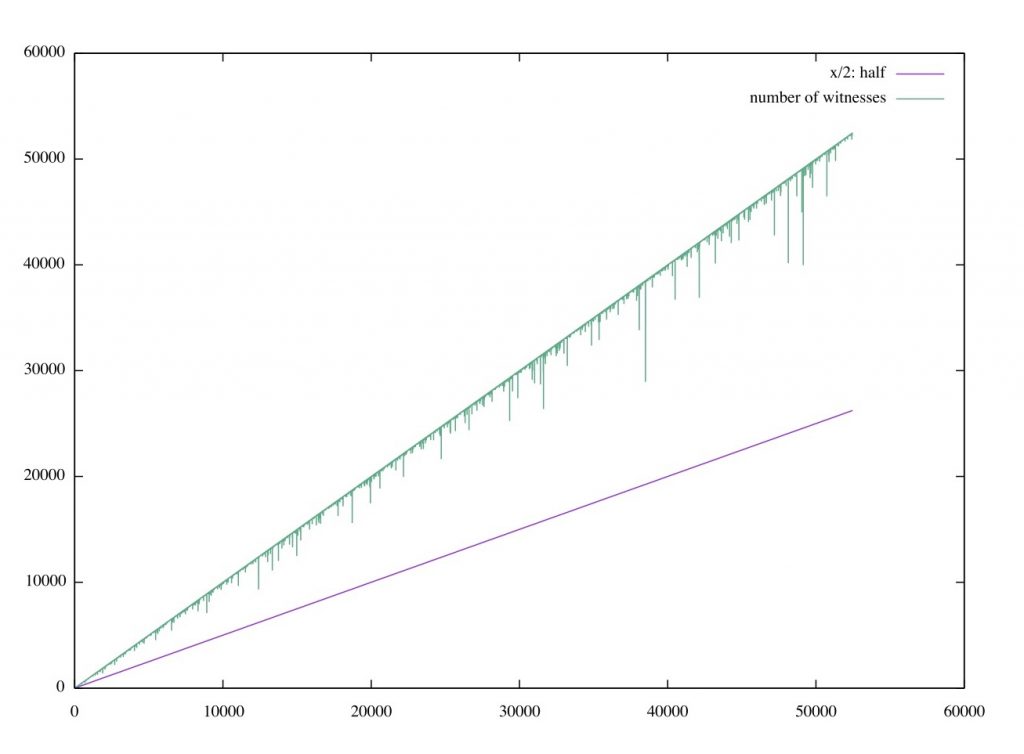
The Rabin Miller algorithm for primality testing relies on a random selection of a’s for which it performs some basic tests in order to determine whether the input n is prime or composite. If n is prime, all a’s work, but if n is composite it is possible to show that at least half of the a’s work, i.e., at least half of the a’s are witnesses of compositness. But in fact, it seems like a lot more a’s than just half of those in the set {1,2,…,n-1} work; see the following diagram where I test all composites under about 60,000. It is clear that there are more good witnesses than just half the numbers.